プリキュアで学ぶ劣モジュラ関数 - むしゃくしゃしてやった，今は反省している日記

Machine Learning Advent Calendar 2015 1日目の企画です．

機械学習・人工知能系の国際会議（ICML, NIPS, AAAIなど）のチュートリアルや論文を眺めたことのある人なら，Submodular Function（劣モジュラ関数）という単語に見覚えがあるかもしれません．実際，ICML 2013，AAAI 2015や今年のIBISでも劣モジュラ関数のチュートリアル講演がなされています．今回は，劣モジュラ関数についてプリキュアで解説したいと思います．

劣モジュラ関数とは

劣モジュラ関数は集合関数（ある集合の部分集合を引数に取り，実数値を返す関数）の一種です．具体的には以下の定義を満たす関数です．

$f: 2^E \to \mathbb{R}$ が劣モジュラ関数
$\iff$ 全ての$X \subseteq Y$ と $i \not\in Y$ に対して
\[
f(X \cup \{ i \}) - f(X) \geq f(Y \cup \{ i \}) - f(Y)
\]

注: $2^E$ は $E$ の全ての部分集合の集合を表す記号です．

はい，全然分からん！そこでプリキュアの出番です．

$E$ を全てのプリキュアの集合としましょう．つまり
$E =$ {キュアブラック, キュアホワイト, ... , キュアスカーレット }
です．

（↓$E$のイメージ図）

劇場版シリーズ最新作『映画プリキュアオールスターズ　みんなで歌う♪奇跡の魔法！』2016年3月19日（土）全国劇場にて公開決定！「プリキュア」シリーズ劇場作品20作目！#precure https://t.co/WAhtg1Thas pic.twitter.com/Bu6kIsMtve
— 東映アニメーション (@toeianime_info) 2015, 11月 28

プリキュアを何人か集めてきた集合を $X$ としたとき，その中に含まれるプリキュアの色の種類を $f(X)$ として定義します．

たとえば
$X =$ {キュアマリン(青), キュアピーチ(桃), キュアピース(黄), キュアフローラ(桃)}
にすると，$X$には全部で3色のプリキュアがいるので $f(X) = 3$ です．

$X$ を含む集合として
$Y =$ {キュアマリン(青), キュアピーチ(桃), キュアピース(黄), キュアフローラ(桃), キュアミント(緑), キュアエース(赤)}
を取ると，今度は $f(Y) = 5$ です．

ここで，$X$ と $Y$ にキュアマーチ(緑)を足して，$f$ の値がどう変化するかをみてみます（つまり $i =$ キュアマーチ）．
$X \cup \{ i \} =$ {キュアマリン(青), キュアピーチ(桃), キュアピース(黄), キュアフローラ(桃), キュアマーチ(緑)}
ですから，$f$ の値は1増えます．
一方で，
$Y \cup \{ i \} =$ {キュアマリン(青), キュアピーチ(桃), キュアピース(黄), キュアフローラ(桃), キュアミント(緑), キュアエース(赤), キュアマーチ(緑)}
ですが，$Y$ には既に緑のキュアミントがいるので，$f$ の値は変化しません．

この例で分かるとおり，$X \subseteq Y$ を満たす2つの集合 $X$, $Y$ に新しい要素 $i$ を追加したとき，色の増え方は必ず ($X$ に対する増え方) $\geq$ ($Y$ に対する増え方) になります．これが上の定義が言っていることです．
つまり，劣モジュラ関数は，手持ちの集合が大きくなればなるほど増え方が鈍っていく関数*1です．

ちなみに，この関数は $X \subseteq Y$ ならば $f(X) \leq f(Y)$ という性質（単調性）も持っていますが，劣モジュラ関数が必ず単調であるとは限りません．ただし，以下で見るように，単調な劣モジュラ関数でも機械学習にたくさんの応用があります．

応用例: センサー配置問題

有名な応用としてセンサー配置問題があります．ここではセンサーの代わりにプリキュアを配置することにしましょう．賢いゆいちゃんは，街にゼツボーグが出てきたときのために，プリキュアを事前に配置して迎え撃つことにしました．過去の出現パターンから，ゼツボーグが出てくる可能性のある場所（候補点）はある程度絞り込めたとします．

プリキュアは人目についてはいけないので，配置できる場所は限られますが，ある程度の範囲ならプリキュア1人でカバーできます．さて，4人のプリキュアをどこに配置したら最も多くの候補点をカバーできるでしょうか？

f:id:tasusu:20151130014227p:plain

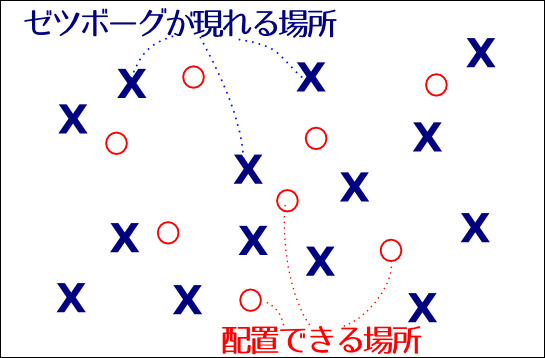
たとえばこんな配置が考えられます．この配置だと9箇所カバーできています．
f:id:tasusu:20151130014335p:plain

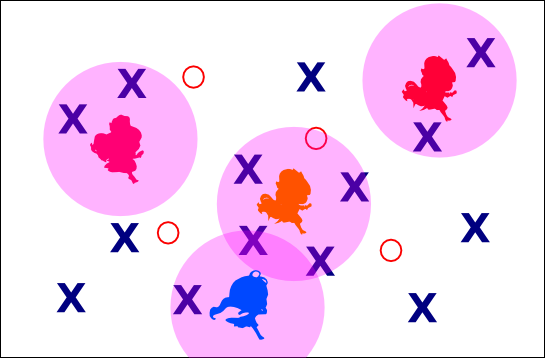
この例では $E$ をプリキュアを配置できる座標の集合, $f(X)$ を配置 $X$ によってカバーされる候補点の数とすると，実は $f$ は単調な劣モジュラ関数になります．そして，この問題は

$|X| \leq 4$ という制約のもとで $f(X)$ を最大化せよ

という問題になります．

このように単調な劣モジュラ関数 $f$ に対して

$|X| \leq k$ という制約のもとで $f(X)$ を最大化せよ

という問題は，単調劣モジュラ関数最大化と呼ばれ，貪欲法とよばれる非常に実用的なアルゴリズムが知られています．

貪欲法は，$X = \emptyset$ からスタートして，$f(X \cup \{s\}) - f(X)$ が最大となる $s$ を選んで $X$ に追加することを $k$ 回繰り返すだけの非常にシンプルなアルゴリズムです．
しかしながら性能は驚くほど高く，理論的には最悪でも最適値の 1-1/e ≒ 63% の解を出力することが保証されており，経験的には最適値の90%〜ほぼ100%に近い解を出力します．
貪欲法のおかげで，単調劣モジュラ関数最大化は「実用上解けるNP困難問題」として